
- 머신러닝은 데이터 가공/변환, 모델 학습/예측, 그리고 평가의 프로세스로 구성된다. 앞서 게시한 타이타닉 데이터 실습에서는 모델 예측 성능 평가를 위해 정확도를 이용했다.
- 머신러닝 모델은 정확도 외에도 여러 방법으로 예측 성능을 평가할 수 있다. 일반적으로 모델이 분류냐 회귀냐에 따라 여러 종류로 나뉜다. 회귀의 경우 대부분 실제값과 예측값의 오차 평균값에 기반한다.
1. 성능평가 - 회귀 모형 오차의 개념
- 오차는 실제값과 예측값의 차이를 말함, 양의 값과 음의 값이 발생
- 회귀 모형은 오차의 제곱 혹은 절대값의 합이 `최소화되는 라인`을 찾는 것이 목표


- 회귀 모형 성능평가에서 루트를 씌우거나, 절대값을 취하는 이유는 다음의 표 예시를 보면 알 수 있다.
| 실제값 | 예측치1 | 오차1 | 예측치2 | 오차2 |
| 25 | 20 | 5 | 10 | 10 |
| 30 | 33 | -3 | 2 | 2 |
| 15 | 13 | 2 | 0 | 0 |
| 16 | 11 | 5 | 2 | 2 |
| 22 | 29 | -7 | -12 | -12 |
- 예측 모델 1 과 2의 오차 합은 각 2로 같다
- 하지만 절대값의 합으로 바뀌게 되면 22(=5+3+2+5+7) < 26(=10+2+2+12) 로 변환되어, 두 모델의 평가가 가능해진다.
- MAE1( 4.4 ) < MAE2 ( 5.2 )
- 한편 루트를 씌우는 경우에는 이상치를 조금이나마 보정하기 위한 경우이다.
* 회귀 평가 방법
1. MAE(Mean Absolute Error)

- 활용 코드
from sklearn.metrics import mean_absolute_error
mae = mean_absolute_error(y_test, y_pred)
2. MSE(Mean Squared Error)

- 활용 코드
from sklearn.metrics import mean_squared_error
mae = mean_squared_error (y_test, y_pred)
3. RMSE(Root Mean Squared Error)

- 활용 코드
from sklearn.metrics import mean_squared_error
import numpy as np
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
4. MSLE(Mean Squared Log Error)

- 활용 코드
from sklearn.metrics import mean_squared_log_error
msle = mean_squared_log_error(y_test, y_pred)
msle
5. MAPE(Mean Absolute Error)

- 활용 코드
import numpy as np
def MAPE(y_test, y_pred):
mape = np.mean(np.abs((y_test - y_pred) / y_test)) * 100
return mape
mape = MAPE(y_test, y_pred)
mape
6. 결정계수(𝑅 2)
- 결정계수는 회귀모형을 할 때만 사용한다
- DecisionTree / LightGBM / RandomForest 를 사용한 경우 결정계수를 사용하면 안 된다.


- 활용 코드
from sklearn.metrics import r2_score
r2 = r2_score(y_test, y_pred)
r2
* 분류 평가 방법
- 혼동행렬(Confusion Matrix)
| 예측 결과 | |||
| TRUE | FALSE | ||
| 실제 정답 | TRUE | TP(True Positive) | FN(False Negative) |
| FALSE | FP(False Positive) | TN(True Negative) | |
- 정확도(Accuracy)

- 정밀도(Precision)
- 분모가 작아질수록 값은 커지므로, 정밀도는 실제로 음성(F)인데 양성이라고 한 수치(FP)가 낮아야 커진다.
- ex) 대출심사는 대출 적격자가 아닌 사람에게 돈을 빌려주는 것(FP)과 대출 적격자인데 돈을 빌려주지 않는 것(FN) 중 전자의 경우가 더 큰 문제를 일으킨다.

- 재현율(Recall)
- 분모가 작아질수록 값은 커지므로, 정밀도는 실제로 양성(T)인데 음성이라고 한 수치(FN)가 낮아야 커진다.
- ex) 병원에서 정밀 검사 필요성을 판단할 경우 병이 없지만 검사를 해보자고 하는 것(FP)과 병이 있는데도 검사를 하지 않는 것(FN) 중 후자의 경우가 더 큰 문제를 일으킨다.

* 정밀도 와 재현율은 trade off 의 관계임.
- F1 Score
- 정밀도와 재현율이 어느 한쪽으로 치우치지 않는 수치를 나타낼 때 상대적으로 높은 값을 가진다.
- F1 스코어는 정밀도와 재현율 사이의 균형을 고려하여 하나의 지표로 제공하므로, 특히 클래스 간 불균형이 있는 분류 작업에서 모델의 성능을 평가하는 유용한 도구이다.

- ROC-Curve (<---TN : 특이도, 재현율 : 민감도), 모형의 신뢰성 파악
- 일반적으로 의학 분야에서 많이 사용되지만, 머신러닝의 이진 분류 모델의 예측 성능을 판단하는 중요한 평가 지표이기도 하다.
- AUC는 그러한 ROC 곡선 이하의 면적을 나타낸다. 최저 값은 동전을 무작위로 던져 앞/뒤를 맞추는 랜덤수준의 이진 분류인 0.5이다.

* 일반적으로 분류 모형 판단 기준은 F1 score > AUC > 정확도
= F1 score에 정밀도와 재현율이 포함된 것이므로
* 실무에서는 FN 수치와 FP 수치중 하나를 극단적으로 내리는 경우를 선호하기도 함(위의 사례 같은)
* 피마 인디언 당뇨병 예측 데이터 실습
0. 데이터 불러오기

1. 데이터 파악

2. 데이터셋 분리
- 당뇨 여부 outcome 을 y, 나머지를 x로 y는 층화추출을 실시함.

3. 로지스틱 회귀로 학습, 예측, 평가 진행


- 수정된 get_clf_eval() 함수를 살펴보면, 혼동행렬 / 정확도 / 정밀도 / 재현율 / F1 score를 구할 때는 범주예측값(pred)이 사용되고, ROC / AUC에는 확률값(pred_proba)이 사용된다는 것을 참고하자.



- 재현율이 현저히 낮기 때문에, 임곗값에대한 조정을 검토가 필요해보인다. 먼저 정밀도 재현율 곡선을 보고 변화 추이를 살펴보자.

- 두 곡선의 접점인 임곗값 0.38정도로 낮추면 두 수치는 어느정도 균형을 이루게 되지만, 두 지표 모두 0.7이 안되는 수치로 보인다. 또한 당뇨병 예측이라는 모델 특성상 정밀도보다는 재현율을 좀 더 높여야하는 등 아직 부족한 점이 있다.

4. 데이터 상세하게 파악하기(면밀히 점검)
- 임곗값을 인위적으로 조작하기 전, 다시 데이터 값을 점검해보자. describe() 메서드로 다음과 같이 피처 값의 분포도를 살펴볼 수 있다.
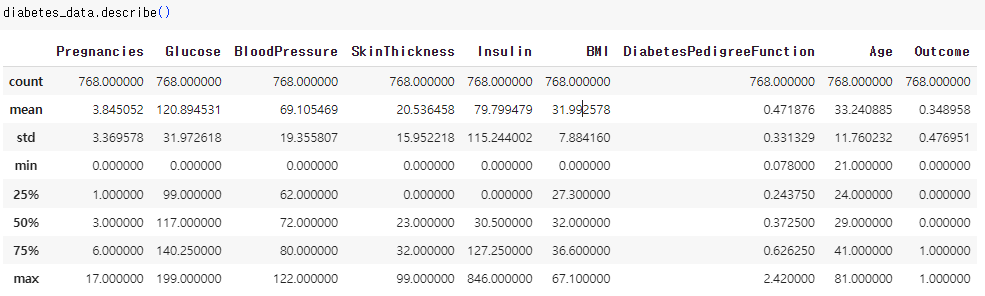
- 아까 info()메서드를 통해 알아본 결과로는 null 값이 없어 일단 지나갔으나 , 피처에 이상한 값들이 있는 것을 확인할 수 있다. Glucose 는 포도당값인데, min이 0으로 존재하는 것을 확인하였다.
-시각화를 통해 보다 확실하게 확인할 수도 있다.
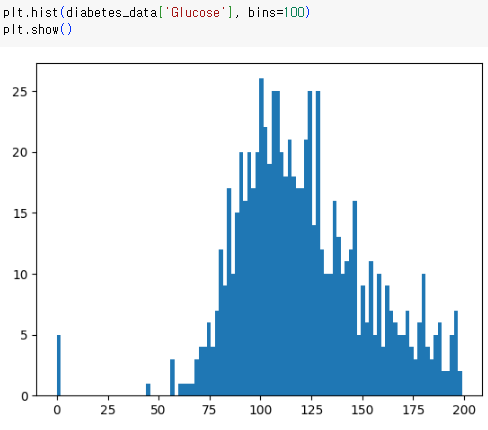
- 이어서 Glucose 뿐만아니라 min 값이 0으로 되어있는 피처 "BloodPressure, SkinThickness, Insulin, BMI" 에 대해 검사를 실시해보도록 하자.

5. 데이터 대체
특히 SkinThickness 와 Insulin은 각 29.56%와 48.7%로 대단히 많은 비중을 차지하는 것을 확인했다. 그래서 삭제하기에는 원할하게 학습하기 어려우므로 .. 해당 피처들의 0 값을 평균값으로 대체해보도록 하자.

- 방금 전과 같은 방식으로 값 대체가 잘 되었는지 확인

6. 데이터 분리 2
- 추가된 StandardScaler의 이유는 앞서 나왔던 수치들의 단위가 다르기 때문이다.

7. 로지스틱 회귀 학습, 예측, 평가 진행 2
- 전체적으로 수치들이 많이 올라갔지만 여전히 재현율은 다소 낮은 상태임을 확인해볼 수 있다.

8. 분류 결정 임곗값 확인
- 다음은 임곗값을 변경하면 평가지표들이 어떻게 변화하는지를 알려주는 코드이다.

8-1 코드 결과값 정리
- 재현율을 높이는 데 가장 좋은 임곗값은 0.33이고, 전체적인 성능이 다 좋아지는 임곗값은 0.48이다.

9. 최종 임곗값 선택
- 무슨 분류를 하는지에 따라 극단적인 임계값이 더 좋게 판단될 수도 있겠으나, 일단은 일반적인 임곗값을 선택해보도록 하겠다.
- 사이킷런의 predict() 메서드는 임곗값을 마음대로 변환할 수 없으므로, Binarizer 클래스를 이용하여 predict_proba()로 추출한 예측 결과 확률값을 변환해 변경된 임곗값에 따른 값을 구해보도록 하자.


이 글은 파이썬 머신러닝 완벽 가이드 개정 2판(권철민, 2022)을 일부 참고하여 작성하였습니다.
'IT & 개발공부 > 파이썬(Python)' 카테고리의 다른 글
| 머신러닝 코드 실습 - 결정트리 & 과적합 (0) | 2023.08.22 |
|---|---|
| 머신러닝 알고리즘(선형회귀, 결정트리 등) 이해하기 (0) | 2023.08.21 |
| 머신러닝 실습 (타이타닉 생존자 예측) (1) | 2023.08.19 |
| 머신러닝에서의 데이터 전처리 (0) | 2023.08.18 |
| 머신러닝과 교차검증(+ 하이퍼 파라미터 튜닝) (0) | 2023.08.17 |



